Caracterización energética de las precipitaciones en la erosión de la cuenca del Cuyaguateje

Rainfall energy characterization in Cuyaguateje basin erosion

Yeleine Almoza Hernández,^I Wim M. Cornelis,^II Hanoi Medina González,^I Maria E. Ruiz Pérez,^I Gustavo Alonso Brito,^I Jorge Díaz Suareza,^I Donald Gabriels^II

^IUniversidad Agraria de la Habana, Grupo de Investigaciones Agrofísicas, Autopista Nacional km 23 y 1/2, San José de las Lajas, Mayabeque, Cuba.

^IIGhent University, Department of Soil Management, Coupure links 653, Ghent, Belgium.

RESUMEN

En Cuba, una de las regiones priorizadas en términos de erosión hídrica es la cuenca del río Cuyaguateje, donde más del 85 % de su suelo presenta alto riesgo de erosión por estar bajo intensas prácticas de laboreo. Los altos acumulados de precipitaciones registrados junto a la no uniformidad de la topografía hacen necesaria una caracterización espacial de la erosividad de las lluvias en el área, ya que constituye un factor fundamental de la erosión. Los objetivos de este trabajo fueron: (a) comparar expresiones que estiman la energía cinética, desde la intensidad de las precipitaciones en la cuenca bajo estudio; (b) desarrollar y validar la relación entre los acumulados de precipitación y el factor R del Modelo RUSLE (Ecuación de Perdidas de Suelo Universal Revisada) (EI₃₀); (c) comparar resultados y tendencias entre R y el Índice Modificado de Fournier MFI así como con el Índice de Lal, AI_m (EI_7.5); (d) presentar los mapas de erosividad de las precipitaciones, según cada índice calculado. Fueron utilizados datos de dos estaciones pluviográficas de la cuenca para calcular R (usando las  ecuaciones de energía cinética de Brown y Foster y la de Kinnell) y AI_m y datos de 26 estaciones pluviométricas a lo largo de toda la cuenca. Como resultado se obtuvo valores de R entre 8284 y 22044 MJ mm ha^-1 h^-1yr^-1 mediante las dos ecuaciones de energía cinética, con los valores más elevados de erosividad en la parte alta o montañosa y los valores más bajos en la parte baja de la cuenca. Alrededor del 96 % del área de la cuenca está afectada por las precipitaciones con alto potencial erosivo. Las correlaciones entre el factor R de RUSLE y el resto de los índices calculados (MFI y AI_m) fueron altas, más de 0,9.

Palabras clave: energía cinética, intensidad, precipitaciones, erosión del suelo.

ABSTRACT

In Cuba, one of the prioritized regions in terms of water erosion is “Cuyaguateje” river basin, where more than 85 % of its soil shows a high erosion risk subjected to intensive farming practices. High pluviometric values registered together with the non-uniform topography necessitate spatially characterised rain erosivity in this area, as it constitutes an essential factor of soil erosion. The objectives of this paper were: (a) to compare expressions that predict kinetic energy from rainfall intensity in our basin of interest, (b) to develop and validate the relationship between cumulative rainfall and R factor from RUSLE (Revised Universal Soil Loss Equation) (EI₃₀), (c) to compare results and trends between R and the Modified Fournier Index MFI, as well as with Lal’s index AI_m (EI7.5), (d) to present rainfall erosivity maps, according to each index calculated. Data from two pluviographic stations were used to calculate R (by Brown and Foster’s also Kinnell’s kinetic energy equations) and AI_m, besides data from 26 pluviometric stations located along the basin of interest. Thus, R values ranged between 8284 and 22044 MJ mm ha^-1 h^-1yr^-1 through both kinetic energy equations, with the highest erosivity values at the top or mountainous part and the lowest values at the basin bottom. Around 96 % of the basin area is affected by rainfall with high erosive potential. Correlations between R factor from RUSLE and the other indexes calculated (MFI and AI_m) were higher than 0,9.

Key words: kinetic energy, intensity, rainfall, soil erosion.

INTRODUCCIÓN

A partir de la década del 80 se han desarrollado muchos trabajos científicos relacionados con la erosión del suelo y muy especialmente con la influencia de precipitaciones, algunos autores (1, 2), hasta la actualidad, como los investigadores de la India (3) han desarrollado nuevos RS-GIS, un método sencillo que ha sido propuesto para la estimación de la erosión del banco. Este método no necesita investigación de campo intenso y puede proporcionar la vulnerabilidad a la erosión de determinada zona cercana a los ríos.

El problema ambiental más grave en Cuba es la degradación del suelo, que es en gran medida debido a la alta erosividad de los eventos de lluvia^A. El CITMA informó que alrededor del 70 % de la superficie cultivada sufre de la degradación del suelo, y aproximadamente el 43 % de esta superficie se somete de media a fuerte erosión hídrica.

Un programa dirigido a promover la gestión sostenible de las cuencas hidrográficas, en particular aquellas cuencas de mayor importancia social, económica y ambiental se estableció hace más de una década. Una de las regiones priorizadas es la cuenca del Cuyaguateje, que está entre las ocho cuencas más importantes del país y se encuentra en la parte occidental de Cuba (al oeste de La Habana). Un área importante de la cuenca del Cuyaguateje se ha erosionado fuertemente de acuerdo con la Academia de Ciencias de Cuba^B. Recientemente, cálculos aproximados por algunos autores indican que el 22 % de la superficie total de la cuenca y el 86 % de la tierra cultivable mostraron un muy alto riesgo de erosión bajo las prácticas actuales de uso de la tierra (4).

Una herramienta adoptada ampliamente en el establecimiento de planes de control de la erosión son los modelos. Ellos permiten estimar las áreas con erosión real y con problemas potenciales de erosión, así como el efecto de las medidas de control a través del análisis de los escenarios (5, 6). Existe una variedad de modelos de erosión, desde los más simples como USLE (7) y RUSLE (5) a otros más complejos como WAST (8), entre muchos otros. Estos modelos se han desarrollado principalmente sobre la base de métodos estadísticos o de observaciones empíricas.

Los modelos empíricos tienen generalmente una estructura mucho más simple, requieren menos parámetros de entrada y muestran un rendimiento en cuanto a la precisión de la predicción de los modelos deterministas cuando se consideran los promedios anuales y muestran un bajo grado de propagación de errores, de acuerdo a las obras llevadas a cabo (9). El modelo empírico RUSLE por sus siglas en Inglés (Revised Universal Soil Loss Equation) estima la pérdida de suelo teniendo en cuenta factores como la topografía, la erodibilidad del suelo, la vegetación, manejo del suelo y la erosividad de las precipitaciones (factor R). Debido a su amplio uso y simplicidad, este modelo ha sido elegido para la evaluación del riesgo de erosión en la cuenca del Cuyaguateje (4).

La evaluación del riesgo de erosión depende, en gran medida, de la caracterización espacial y temporal adecuada de la erosividad de las lluvias. Varios estudios sugieren que la relación entre la precipitación y la respuesta en términos de erosión se determina no sólo por la lluvia acumulada, sino también por la  velocidad de caída de las gotas de lluvia.

La combinación de este último con el diámetro de la gota proporcionada por mediciones de la distribución de tamaño de gota y la energía cinética, se han propuesto como indicadores para la erosividad de la lluvia por muchos autores (5), que propusieron multiplicar la energía cinética E con la intensidad de lluvia máxima, resultado en I₃₀ intensidad de lluvia de 30 minutos en lo que se conoce como EI₃₀. Este parámetro corresponde al factor de erosividad en (R) USLE. Los valores de intensidad se tienen que derivar de los datos pluviográficos.

Determinar la energía cinética de un evento de lluvia desde el tamaño y la velocidad de caída de cada gota de agua que comprende el evento, es poco práctico, y por lo tanto, se han desarrollado parametrizaciones para deducir empíricamente a partir de datos de intensidad. Ejemplos de tales relaciones aplicables para las diversas regiones fueron mostradas en diferentes estudios (10, 11, 12).

En la revisión de los estudios de 19 ubicaciones en todo el mundo (12), se encontró que la relación de la intensidad con la energía (IE) establecida sobre la base de datos de Miami FL, EE.UU. (1)  (que se supone que tiene un clima similar al de nuestra área de estudio, el oeste de Cuba), fue sustancialmente diferente (10 %), a partir de las relaciones presentadas (9), en base a datos de Washington DC, EE.UU. y usados en USLE (2) sobre la base de datos de Holly Springs MS, EE.UU. y utilizado en RUSLE (5), cuando se comparan con los datos de energía de la tormenta (24 tormentas) recogidos en Gunnedah, el sudeste de Australia (13). En el mismo estudio (1, 12), the Kinnell la relación E-I difería con casi el 15 %, a partir de una ecuación generalizada que deriva después de haber examinado los diferentes conjuntos de datos de todo el mundo.

Las estimaciones altas de E derivados de la Florida, con clima subtropical húmedo se asociaron principalmente con el alto contenido de energía cinética, predicho a bajas intensidades de precipitación (12). Los mismos autores argumentaron, además, que las relaciones E-I exponenciales, resultan más adecuados que las estimaciones por las ecuaciones de las relaciones logarítmicas (1, 2). Cabe señalar que en las relaciones E representa la cantidad de energía cinética gastada por unidad de volumen de lluvia (1, 2).

Otros estudios argumentaron que es estadísticamente más apropiado para expresar E en términos de energía cinética por unidad de área y por unidad de tiempo en relación con la I (11). También demostraron que, al considerar los modelos de distribución de tamaño de  gota, es más adecuado vincular el tiempo específico-E e I con una ley de potencia. Tal expresión de la ley de energía fue utilizada para estimar E-tiempo específico para la Florida, EE.UU (14).

Aparte de las diferencias espaciales por ubicación geográfica o por el tipo de lluvia (11), las diferencias temporales en la erosividad de lluvias son comunes. Por ejemplo, en la región de la cuenca Dos Quebradas en la región cafetalera central de Colombia se calculó el EI₃₀, con una precipitación anual de 2,600-3,200 mm. Con este trabajo de investigación se determinó que las tormentas individuales representan tanto como el 25 % de los EI₃₀ (10,409-15,975 MJ mm ha^-1 h^-1 año^-1) y presentó grandes diferencias anuales entre los modelos de erosividad en las temporadas húmeda y seca.

Para eludir la necesidad de la energía cinética para calcular la erosividad, se utilizó el índice Lal,
AI_m (15), derivada de los datos procedentes de Nigeria. Es el producto de los acumulados de lluvia para la intensidad máxima de 7,5 minutos.

Sin embargo, las series de datos necesarios para derivar R y AI_m  a menudo no están disponibles en una escala de alta resolución. Por lo tanto, se han introducido otros índices de erosividad. Un índice popular es el índice modificado Fournier (16), MFI, originalmente desarrollado para Marruecos. MFI es la suma de la precipitación mensual cuadrado sobre precipitación anual; muchos autores llegaron a la conclusión de que, MFI representa un índice de erosividad pobre. Por otra parte, se han desarrollado modelos que predicen R de la cantidad de lluvia; por ejemplo, en la zona del Mediterráneo (17, 18, 19), en Nigeria (15, 20), en Irán (21, 22), en Kenia (23, 24) y en España (15). Las diferencias en los parámetros del modelo sugieren que estas relaciones están hechas para un sitio o región específica (15).

El objetivo general de este estudio fue evaluar la erosividad espacial y temporal en la cuenca del río Cuyaguateje en la parte occidental de Cuba. Al igual que en la mayoría de las regiones del mundo, son raros los datos pluviográficos en series de tiempo suficientemente largo y de alta resolución especial para permitir la interpolación espacial. Los objetivos específicos de este trabajo fueron: (a) comparar expresiones que predicen la energía cinética de la intensidad de lluvia relevante para la cuenca de interés; (b) desarrollar y validar una relación específica de la región entre RUSLE R y la cantidad de lluvia disponible de estaciones pluviométricas; (c) comparar las tendencias en R con IMF y AI_m; (d) presentar mapas de erosividad en base a los indicadores anteriores.

MATERIALES Y MÉTODOS

Área de estudio

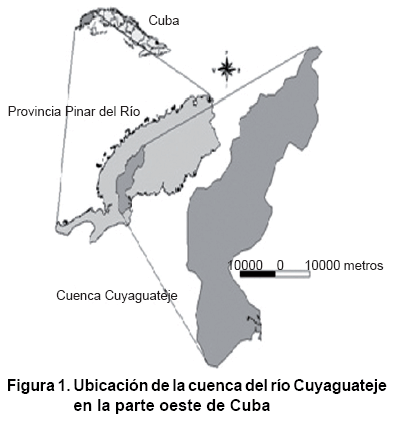
La cuenca del río Cuyaguateje tiene una superficie de 723 km², con una longitud total de río de 112,4 kilómetros desde su origen en el “Cerro Cabras” hacia abajo hasta su desembocadura en el mar Caribe^C. La cuenca se encuentra en la provincia de Pinar del Río, en el occidente de Cuba (Figura 1). Es como el resto de Cuba, sometida a un clima tropical. Una estación seca bien definida, que dura de noviembre a abril y la precipitación media anual es de 1,766 mm. La temperatura media anual es de 25,1 °C, y varía de 22,0 °C en enero a 27,7 °C en julio y agosto. La humedad relativa es de alrededor de 77 % en la estación seca y alrededor de 82 % durante el resto del año (temporada de lluvias.)

Esta cuenca se caracteriza por estar en la cadena montañosa de la Cordillera de Guaniguanico. En su parte norte, la Sierra de los Órganos, se caracteriza por colinas empinadas con lados de piedra caliza (mogotes) y numerosos valles cultivados. Esta región cársica ha sufrido intensa erosión (geológica) y tiene un extenso sistema de drenaje subterráneo. A ambos lados de este sitio las Alturas de Pizarras forman un paisaje montañoso que también está gravemente erosionado y sus pocos suelos desarrollados se componen de pizarras, esquistos y arena. La parte sur de la cuenca se caracteriza por una llanura de tierras bajas de arena, Llanura Costera Sur. La elevación varía entre 0 a 589 m sobre el nivel del mar, con una altura media de 124 m^C.

De acuerdo con el mapa de suelos (escala 1: 25000) del Instituto de Suelos, los principales tipos de suelos de la región son Ferrasoles y Leptosols^C. La tierra se debe principalmente al cultivo de tabaco, frijoles, maíz, bosques de barbecho y pinos (Pinus caribea L. y Pinus tropicalis (4).

Registros de lluvia

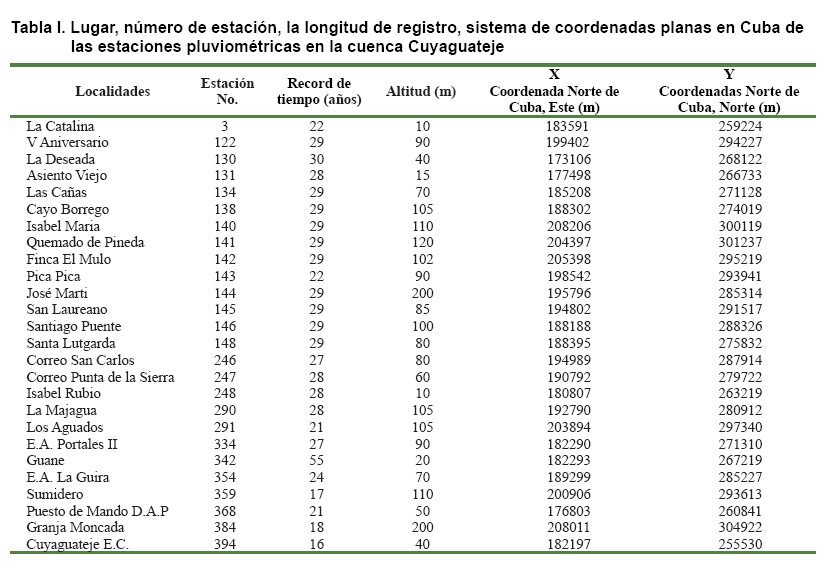
Los datos de precipitación diaria de 26 estaciones pluviométricas estaban disponibles, pero sólo tres estaciones proporcionaron datos pluviográficos. Todos los datos pluviométricos y pluviográficos fueron proporcionados por el Instituto Nacional de Recursos Hidráulicos (INRH). La longitud de la serie de datos, su ubicación, altitud, posición y la precipitación anual promedio se muestran en la Tabla I. Su distribución espacial sobre la cuenca se muestra en la Figura 2. Sólo años con registros de precipitación completas fueron retenidos, lo que dio lugar a longitudes de registro por estación que varía entre los años 1965 y 1992. Las estaciones con datos pluviográficos utilizadas fueron V Aniversario (estación 122; 1964-1992) y Portales II (estación 334; 1964-1992). También es importante señalar que después de la crisis económica de los años 90 en Cuba, se detuvo la medición gradual de los registros de precipitación en las estaciones experimentales. No existen registros actualizados. En la actualidad el INRH está trabajando en ello.

Las relaciones de intensidad de la energía cinética de precipitaciones

Se utilizó la ecuación propuesta en el manual RUSLE (6) que sugiere la ecuación exponencial (2) para calcular el e_k energía cinética por pluviofase k (MJ ha^-1 mm^-1), desde el i_k que es la intensidad de lluvia en el pluviofase k (en mm h^-1) (1).

(Ecuación 1) e_k=0,29 [1-0,72 exp (-0,05i_k).

Como se ha dicho, esta ecuación se creó utilizando datos de Mississippi, EE.UU. sugeridos para la Florida, EE.UU.

Por otro lado se utilizó también la ecuación con una forma similar pero diferente en sus parámetros (sugerida para la Florida, EE.UU.):

(Ecuación 2) e_k=0,2931[1-0,281exp (-0,018i_k)]

Se utilizó también la ecuación de Smith y De Veaux (14) sugerida para la Florida, EE.UU.:

(Ecuación 3) e_k=0,11i_k^o,14

De acuerdo con los autores (12) se presentó una ecuación general después de haber examinado los conjuntos de datos procedentes de 19 lugares de todo el mundo tomado de la literatura. Esos datos también representan una gran variedad de climas y regiones geográficas.

(Ecuación 4) e_k= 0,28[1-0,52 exp (-0,042i_k)]

Otros autores presentaron una ecuación universal con los parámetros del modelo dependen del tipo de lluvia, considerando las distribuciones del tamaño de gotas existentes de la literatura (11).

Para tormenta convectiva, que se produce típicamente en Cuba (25), sugirieron:

(Ecuación 5) e_k=0,1351i_k^0,1608

La razón para la selección de dos ecuaciones para la Florida, EE.UU., es que, como se ha dicho, presenta un clima bastante similar a la de la zona de estudio.

La Figura 3a muestra la distribución mensual de las precipitaciones en la estación V Aniversario de 1964-1992 (datos del INRH, Cuba), así como en Holly Springs MS, EE.UU. y Miami FL, EE.UU. para 1961-1991 (datos de FAOCLIM Versión 2.02; ). La estación V Aniversario (90 m de altura) y Miami FL (4 m de altitud) muestran patrones de lluvia muy similares, con mayores acumulados para V Aniversario. La Figura 3b muestra la temperatura mensual en los mismos lugares, con valores para V Aniversario tomados de FAOCLIM versión 2.02 (en las inmediaciones Estación de Minas de Matahambre, 13 años). También aquí se puede observar una gran semejanza entre Miami FL y V Aniversario.

Sobre la base de los datos de precipitación y temperatura anteriores, tanto el clima en el V Aniversario y Miami FL puede ser clasificado como Aw (sabana tropical). Aunque el tamaño de gota de la mediana y la energía cinética se han relacionado con la temperatura, el efecto de la temperatura también puede reflejar diferencia en el tipo de tormenta (12).

Por otra parte, la velocidad del viento y la altitud afectan a la energía cinética de las precipitaciones. El viento no solo cambia el tamaño y la distribución de las gotas de lluvia (16), sino también afecta a la energía de impacto de las gotas en la superficie, causando desprendimiento.

Por último, cabe señalar que la Ecuación 5 fue desarrollada utilizando los datos de tamaño de la gotas (27) que fueron obtenidos con una técnica de de cámara de gota para cinco tipos de lluvia (masa de aire, frente frio, frente caliente, onda del este y el canal en alto), que también se están produciendo normalmente en el área de estudio^C. Podríamos, por lo tanto, suponer que la Ecuación 2 es la mejor opción para predecir la energía cinética en el oeste de Cuba.

Antes de estimar el factor R de RUSLE para las tres estaciones pluviográficas (ver sección 2.4), e_k se calcula en primer lugar con las ecuaciones 1-5 para los 11550 pluviofases, que corresponde con las tormentas observadas en V Aniversario (estación 122), durante el período de 1964 a 1992. Los valores e_k obtenidos fueron utilizados para estimar la tormenta individual EI₃₀ valores (utilizando la Ecuación 7, sección 2.4), que finalmente se utilizaron para la comparación de los modelos E-I y la selección de la más adecuada para el occidente de Cuba.

Cálculo del factor de erosividad R para las estaciones pluviográficas

El factor de erosividad RUSLE R se calculó para las estaciones pluviográficas como Ecuación 5:

(Ecuación 6)

donde:

R: erosividad promediado en n años expresado en MJ mm ha^-1 h^-1.

m: número de eventos de lluvia cada año

_i: el año.

_j: un evento de lluvia.

EI₃₀ es la erosividad de un evento de lluvia expresada en MJ mm ha^-1 h¹.

Valores individuales EI₃₀ de la tormenta se calculan a partir de (5):

(Ecuación 7)

donde:

E: energía cinética total de un evento de lluvia expresa en MJ ha^-1.

I₃₀: intensidad máxima de una precipitación durante 30 minutos en mm.

q: número de pluviophases del evento de lluvia.

e_K: energía cinética por unidad de cantidad de lluvia y la superficie en k pluviophase en MJ ha^-1 mm^-1.

∆V_k: cantidad de lluvia en el k pluviophase en mm. Según lo sugerido (7), omitimos los eventos de lluvia de menos de 12,7 mm en el cálculo del factor de R anual.

Los valores del factor R por evento (EI₃₀) se calcularon utilizando el software programado en lenguaje C que produce un archivo con: 1) el número de evento; 2) evento que comienza; 3) finalización del evento; 4) lluvia por caso; 5) intensidad máxima de una lluvia durante 30 minutos por evento; 6) intensidad máxima de una precipitación durante siete minutos; 7) la energía cinética por caso y, por último, 8) factor RUSLE R por evento.

Cálculo del factor de erosividad R para todas las estaciones

El cálculo del factor R diario de erosividad (R_d) se obtuvo mediante la adición de EI₃₀ valores correspondientes a todos los eventos en un día. Al mismo tiempo, la lluvia correspondiente a cada evento se resumió en totales diarios P_d, R_d y P_d estos fueron agrupados por meses para evaluar el efecto temporal de la erosividad dentro del año.

Sólo se consideraron los datos de V Aniversario. Esta estación fue seleccionada ya que comprendía una serie de tiempo más larga (29 años). Las ecuaciones de regresión desarrolladas entre R_d y P_d para el V Aniversario se validaron para las otras dos estaciones pluviográficas, para las que se contaba con datos de intensidad, una de las cuales se encuentra dentro de la misma subcuenca. Las expresiones matemáticas obtenidas de la relación entre R_d y P_d  se usaron entonces no sólo para calcular la erosividad diaria R_d de las 23 estaciones pluviométricas restantes, sino también para volver a calcular los valores de erosividad diaria para las tres estaciones pluviográficas (utilizando los datos pluviométricos disponibles en aquellas estaciones). Un procedimiento similar se siguió para obtener valores de Rm mensuales y anuales para cada una de las estaciones.

Índice de Fournier Modificado (MFI)

MFI se define como (15):

(Ecuación 8)

donde:

P_i: precipitación en mm del mes I
P: la precipitación media anual en mm
Se calculó para cada estación (n = 26) y se compara con R. anual.

Índice de erosividad Lal

De acuerdo con los autores (16) introdujeron un índice que se puede escribir como:

(Ecuación 9)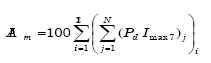

donde:

AI_m: erosividad de la lluvia, expresada en cm² h^-1.

I_{max 7}: intensidad de la precipitación máxima de siete minutos en mm h^-1.

n: número de eventos de lluvia en el mes.

Se aplicó la misma metodología que se utilizó para determinar los valores mensuales de R, pero con la consideración de la intensidad de lluvia máxima en siete minutos, en lugar de a los 30 minutos.

Mapa de la erosividad

La interpolación es un método o función matemática que calcula los valores en los lugares donde no hay valores medidos. Esta puede ser tan simple como una línea de números; sin embargo, la mayoría de la investigación en ciencias de la información geográfica implica datos espaciales. La interpolación espacial asume los datos de atributos que son continuas en el espacio. Los mapas para cada uno de los índices se realizaron utilizando como método de interpolación el Inverso de la Distancia al Cuadrado, por sus siglas en inglés Inverse Distance Weighting (IDW) en Surfer 7.0., se basa en la suposición de que los valores cercanos contribuyen más o tengan más peso que los valores interpolados de observaciones a distancia. En otras palabras, para este método de la influencia de un punto de datos conocido es inversamente proporcional a la distancia desde la ubicación desconocida que se está estimando. La ventaja de IDW es que es intuitiva y eficaz. Esta interpolación funciona mejor con puntos uniformemente distribuidos. De manera similar a las funciones SPLINE, IDW es sensible a los valores atípicos.

RESULTADOS Y DISCUSIÓN

Relación de intensidad de la energía cinética-precipitaciones en la estación V Aniversario

Los datos de la estación pluviográfica V Aniversario para el período 1964-1992 produjeron 2668 tormentas. Graficando de la cantidad de energía cinética consumida por unidad de volumen de lluvia, denotado por e_{k mm}, en función de la intensidad de la lluvia, para cada modelo se muestran grandes diferencias entre ellos (Figura 4a, b), según las intensidades de la cuenca en estudio.

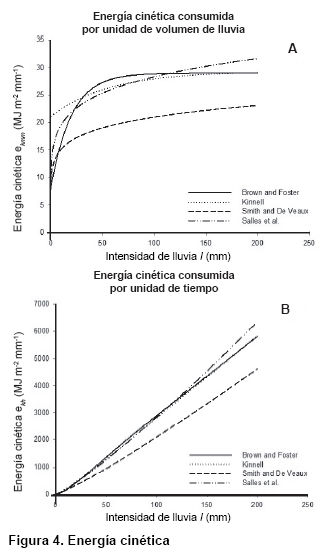
Los modelos exponenciales disminuyeron los valores máximos a intensidades de alrededor de 70 mm h^-1. Se resalta evidencia evidencia sustancial de que el tamaño “máximo” de gota media se alcanza a intensidades superiores a 70-100 mm h^-1 (12). Para intensidades inferiores a 30 mm h^-1, las diferencias entre los modelos fueron muy sustancial. Aunque el 92 % de los pluviophases tenía intensidades menor que I≤30 mm h^-1, la elección del modelo E-I tendrá un impacto menor ya que estas intensidades más bajas se asocian generalmente a bajos acumulados de precipitaciones (18).

En la Figura 5, valores obtenidos de EI₃₀ en los modelos de Miami (Ecuaciones 2-3) se grafican frente a los valores obtenidos a partir de la referencia ‘RUSLE’ EI₃₀ y ecuaciones “generales” (Ecuación 1 y 4-5, respectivamente). Desde nuestra base de datos, los valores estimados con EI₃₀ (1) ecuación para Miami (2) FL parecen ser mayores que los calculados a partir de la ‘RUSLE’ (1) ecuación.

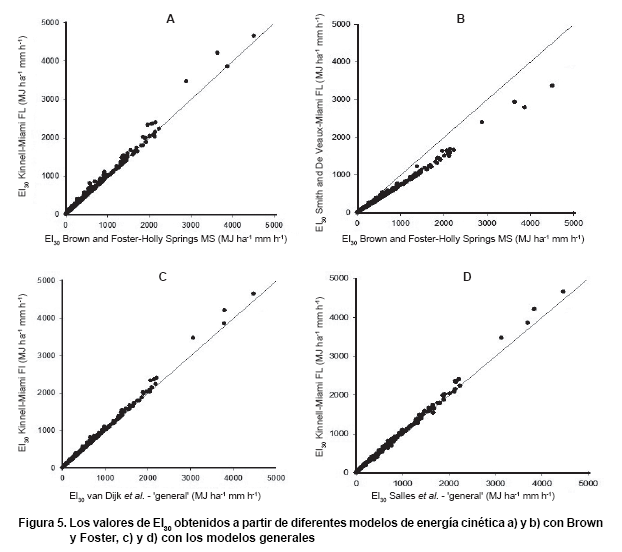
Las desviaciones mayores se observan para los más altos valores de EI₃₀. Estos están asociados con las tormentas de la duración extrema (> 22 horas, un 1,2 % de los eventos) y los eventos de precipitaciones extremas (>200 mm, 0,2 %), pero los valores I₃₀ algo menos extremas (>40 mm h^-1, 7,5 %). Los valores EI₃₀ obtenidos para Miami FL (14) son sorprendentemente mucho más bajos que los calculados (2). Esto se observa en la Figura 4. La razón de la discrepancia aún no está clara. Tal vez un error de escritura de la intersección de la Ecuación 3 podría explicar esta gran diferencia. Ambas ecuaciones “generales” (11, 12), respectivamente, tienen una posición intermedia entre los modelos Kinnel, Brown y Foster.

Cuando se expresa la energía cinética por unidad de área y por unidad de tiempo, e_{k h}, siendo este último igual a e_{k mm} i_k  y se grafica contra intensidad de la lluvia, las diferencias entre los modelos parecen ser más pequeñas (Figura 4a, b), según lo propuesto, se concluye que la energía cinética en unidad de tiempo e_{k h} es más apropiada para ser vinculada a la intensidad  i_k que la propia energía en unidad de volumen e_{k mm} (11). Sin embargo, en sí mismo, las diferencias entre ambas formas de expresar la energía cinética siguen siendo las mismas, pero en el caso de e_{k h}, estas diferencias parecen estar enmascarada por las bajas intensidades que van junto con las grandes desviaciones en la energía cinética que parecen existir entre los modelos a intensidades inferiores a 30 mm h^-1.

La diferencia relativa en R anual entre el modelo Kinnell en una mano y el Brown y Foster, Smith y
D Veaux, van Dijk et al. y Salles et al. en el otro lado, es 4,4 , 28,0 , 4,6  y 4,7 %, respectivamente. Las pequeñas diferencias entre el modelo Kinnell y el Brown y Foster  pueden ser significativas. De acuerdo con lo planteado, a partir de análisis de datos de sudeste de Australia,  se encuentra una diferencia entre ambos de 23 % (13).

Una posible explicación de estas pequeñas diferencias puede ser que para algunas tormentas muy extremas, los datos podrían faltar en nuestro estudio. Durante la tormenta Alberto en 1982, por ejemplo, el técnico responsable de la estación V Aniversario tuvo que escapar de esta porque el agua estaba subiendo muy alto. Justo antes de irse le hizo una última grabación para obtener precipitaciones de 620 mm.

A pesar de existir diferencias en R anual entre el modelo Kinnell y el Brown y Foster, estas fueron relativamente pequeñas (más pequeñas de lo esperado), por lo que decidimos continuar con el modelo desarrollado (1), que fue implementado utilizando datos de Miami FL que, como se ha demostrado anteriormente en este documento, representa condiciones de lluvia semejantes a nuestra área de estudio.

Relaciones erosividad-cantidad de lluvia

La variación observada en la erosividad diaria era en gran medida explicada por los acumulados de lluvia diaria. Nos encontramos así frente a una ley de potencia que describe la relación entre R y P de todos los días de cada mes. Sin embargo, esta ecuación tiende a sobreestimar R_d durante días con P_d superior a 70 mm (fenómenos extremos). Para tales días, una ecuación lineal exhibió los mejores ajustes. Así encontramos:
(Ecuación 10)    for P_d £ 70 mm

(Ecuación 11) for P_d > 70 mm

Debido a la alta variación en la precipitación mensual (Figura 3a), la Ecuación 10 fue arreglado para cada mes. Esto produjo, de acuerdo a una prueba de ANOVA, mejores resultados que cuando se agruparon los datos en una estación húmeda y seca o más de un año completo. En contraste con esto, la solución de la Ecuación 11 sobre un conjunto de datos anuales no dio peores resultados que cuando se divide el conjunto de datos en las estaciones o meses. Luego se obtuvo el mismo tipo de ecuaciones de regresión entre el diario Lal erosividad índice AI_{M D} y P_d:

(Ecuación 12) AI_md = α P^β_d     for P_d £ 70 mm   

(Ecuación 13) AI_md = X P_d+δ   for P_d > 70 mm

En la relación R_d y P_d, para calcular estos valores, en primer lugar se utilizó Rd el modelo de Brow and Foster y después Kinnell. Todo esto para poder obtener dos valores de erosividad para toda la cuenca, para compararlos y finalmente hacer la cartografía.

La Tabla II muestra, los valores de a, b, α y β obtenidos por cada mes (Ecuaciones 10 y 12), valores ‘anuales’ c, d, χ y δ (Ecuaciones 11 y 13) y sus errores estándar y la regresión de coeficientes de determinación.

Se puede observar que el B y b valores de las ecuaciones 10 y 12, para todos los patrones eran entre 2 y 1,70 para todos los meses. Los coeficientes a y amostraron un patrón no estacionario con valores más bajos de noviembre a enero (Tabla II).

Los valores más altos se encontraron de julio a septiembre para todos los modelos, aunque estos meses son más bajos en acumulado respecto a  junio. Este último mes mostró valores a y α similares a febrero, marzo, abril, mayo y octubre, aunque estos meses exponen bastante diferentes patrones de lluvia. Esto significa que por cada mm de lluvia, los tres meses de verano muestran una erosividad sustancialmente más alta que el resto de los meses. La erosividad más baja por mm de lluvia se produce desde noviembre hasta enero. No se capturó el patrón temporal de α y a en la expresión matemática. Conclusiones similares pueden extraerse cuando se considera el índice AI_M de Lal.

En el húmedo Nigeria, fue calculado el factor R a partir del enfoque RUSLE (5), también se obtuvo un valor a de 0,27 y un valor b de 1,94, lo que resulta en un poder erosivo similar por mm de lluvia con el obtenido en el área de estudio (20).

Las ecuaciones de regresión obtenidas anteriormente para la estación V Aniversario fueron validadas por la estación Portales II (334) localizada a 182,290 coordenada Este y coordenada Norte de 271,310 (parte sur de la cuenca).

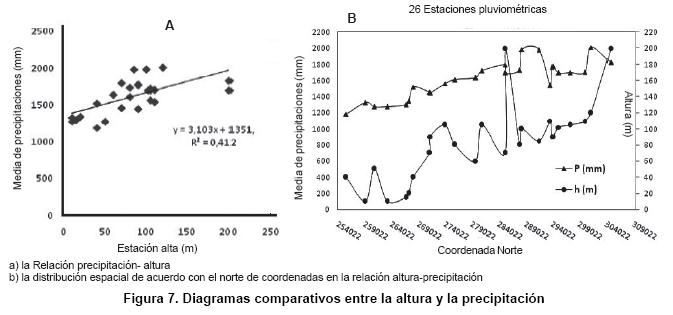
La estación Portales II es la que tiene los datos pluviográficos situados al sur. Sólo existen cuatro estaciones con datos pluviográficos dentro de la cuenca. La validación se llevó a cabo bajo el modelo de R (2). La Figura 6 muestra una buena concordancia entre los valores calculados R_m y los predichos con las ecuaciones 10 y 12, con un R²=0,66, aunque no es muy alta, pero responde satisfactoriamente a la estimación. De hecho, se demostró que la cantidad de lluvia puede ser o no influenciado por la altura en metros, pero no es un factor decisivo en el comportamiento de la misma.

En la Figura 7a se observa el comportamiento de estas dos variables y la ligera tendencia a aumentar de norte a sur la precipitación media. En el eje “x” se representó las coordenadas norte de las 26 estaciones y en el eje “y” las precipitaciones y las alturas correspondientes a cada estación. Sin embargo, en la Figura 7b una relación lineal baja se evidencia con un R² de 0,41 entre la altura y la cantidad de precipitación anual.

Comportamiento temporal y espacial de R en la cuenca del Cuyaguateje

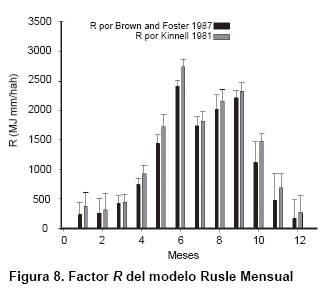
A diferencia de la erosividad por mm de lluvia (es decir, un coeficiente α en la Ecuación 10, erosividad mensual R_m siguió a la distribución mensual de precipitaciones muy bien, con un coeficiente de correlación de 0,98 entre ambos. Junio es el mes con más lluvia erosiva con un valor medio de 2,423 R_m MJ mm ha^-1h^-1 (2) y 2,748 MJ mm ha^-1h^-1 (1), mientras que diciembre es el de menos lluvia erosiva (media R_m=171,1 y 279,9 MJ mm ha^-1 h^-1, respectivamente (Figura 8). La alta erosividad de las lluvias de junio no es debido a una mayor erosividad por mm de lluvia como se ha mencionado anteriormente, sino a las cantidades más altas de precipitaciones y, por lo tanto, la energía cinética mensual más alta. Estos resultados son importantes en la planificación de las actividades agrícolas y de riego para minimizar la erosión del suelo. También AI_m mensual siguieron un patrón similar y se correlacionan bien con P_m (r = 0,90) y a R_m(1) (r = 0,97) y R_m (2) (0,96).

Por estación, los valores medios anuales de Ia erosividad de la lluvia se calcularon a partir de los valores de R_m mensual. La Figura 9 muestra la distribución espacial en el mapa de media anual del factor R (2) y b) el mapa de factor R (2), así como la precipitación anual media y la media de R mensual (2) para la temporada de lluvias (junio-octubre) el mapa y la estación seca (noviembre-mayo); R el comportamiento espacial y temporal fue parecido en esos meses (1).

La Tabla III muestra las medias anuales de P y R para las diferentes estaciones en la cuenca. Dentro de la cuenca, R anual oscila entre un máximo de R de 18,467 MJ mm ha^-1 h^-1 en la estación de San Laureano (número 145) y un mínimo de 8,294 mm MJ ha^-1 h^-1 en Cuyaguateje estación EC (número 394) (Figura 10) (2). Para R fue un mismo comportamiento espacial, siendo el valor máximo en San Laureano con 22,044 MJ mm ha^-1 h^-1 y el valor mínimo en Cuyaguateje E.C. 9673 con MJ mm ha^-1 h^-1 (1).

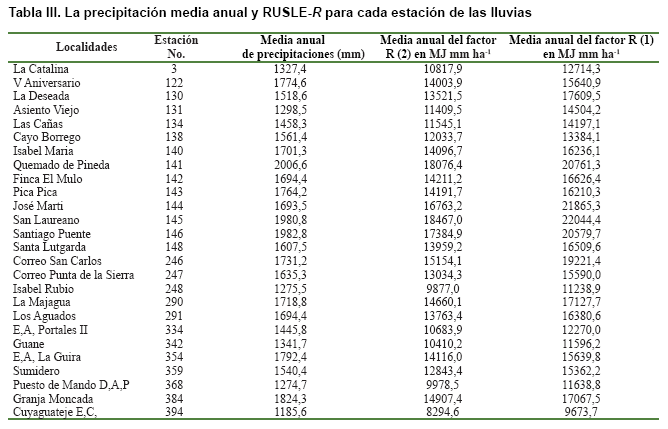
Algunos autores presentan una visión general de los rangos de los valores R de 10 estudios en diferentes regiones tropicales de todo el mundo (9). En comparación con esos valores, el valor R más bajo observado en nuestra cuenca de interés es más grande que los valores mínimos observados en estos estudios.

Otros valores del factor R se registraron en los Andes colombianos (como mínimo R=10,409 MJ mmha^-1 h^-1 y Malasia (mínimo R= 13,600 MJ mmha^-1 h^-1 (28). Todos los demás valores mínimos en ese estudio no excedieron a 6345 MJ mmha^-1 h^-1; del mismo modo, al considerar nuestro valor máximo R, que pertenecía al grupo con los valores más grandes. En Malasia se registró un valor de 21,600 MJ mmha^-1 h^{- 1} (28), en Hawai, un valor de 23,828 MJ mmha^-1 h^-1 (5), y en Australia tropical, un valor de 33,481 MJ mmha^-1 h^-1 (29).

Otros recientes estudios mostraron valores máximos R de 20,035 MJ mm ha^-1 h^-1 en Brasil (30), y 27,808 MJ mm ha^-1 h^-1 en Nigeria (20).

Las tormentas con intensidades de lluvia por debajo de 25 mm h^-1 son no erosivas (23). Los eventos de lluvia de menos de 12,7 mm deben ser omitidos, a no ser que, al menos, 6,35 mm de lluvia cae en 15 minutos (7). La inspección de nuestros registros mostró que sólo el 15,7 % de los eventos tuvo un I₃₀ de más de 25 mm h^-1, mientras que el 26,3 % de los eventos mostró cantidades de lluvia superior a 12,7 mm.

Esto significa que en nuestra cuenca de interés, la mayor parte de las lluvias son no erosivas, pero que en una minoría de los acontecimientos son extremadamente erosivas, lo que le confiere altos valores de erosividad anuales. El valor R más alto de más de 22,000 MJ mmha^-1 h^-1 (2) se observó en San Laureano (estación 145), donde la precipitación anual fue de 1980,8 mm. En el Australia Tropical, por una cantidad similar de P anual, R era mucho menor. Por el contrario, en Nigeria valores de P anuales similares rindierion una erosividad parecida.

Esto demuestra que dentro de las zonas tropicales, existen grandes diferencias en el poder erosivo de las tormentas de lluvia. De todos modos, R anual también se correlaciona bien con P anual (r=0,94) (2).

La Figura 9a muestra que la media anual de erosividad disminuye con la distancia a la desembocadura en el mar Caribe; es decir, a medida que nos alejamos de las zonas más altas.

La estación de San Laureano, donde se encuentra el valor R más alto, no coincide en la Tabla I, con el valor de mayor acumulado, ni es el punto de mayor altitud (85 m). El comportamiento no es tan uniforme entre la altitud y la erosividad en esta cuenca, más podríamos generalizar que al norte hay valores más altos de erosividad y al sur más bajos.

La estación Cuyaguateje E.C. con un valor R más bajo está en la parte baja de la cuenca. Valores de R (2) observados a lo largo de la cuenca muestra un valor medio de 12,895 MJ mm ha^-1 h^-1 con un 20 % de coeficiente de variación y R (1) tiene un valor medio de 15,834 MJ mm ha^-1h^-1 con un 23 % de coeficiente de variación.

De acuerdo con la clasificación de erosividad reportada (31, 32) en la Tabla IV, la mayor parte de la cuenca del río Cuyaguateje tiene una fuerte erosividad. Teniendo en cuenta la distribución de los valores R en la cuenca, al rededor del 96 % de esta área está afectada por una fuerte erosividad por las lluvias.

Los valores medios del índice LAl de Ai_m cambiados aproximadamente de la misma forma como el índice mensual de R (Figura 11A). El coeficiente de correlación entre R mensual (2) y Ai_m mensual fue 0,96 y con R (1) fue 0,97 (Tabla V).

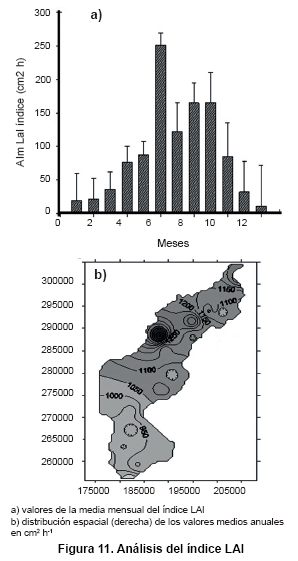
El mayor valor de Ai_m en la cuenca fue 251,3 cm² h^-1 en junio y el valor más bajo observado fue 11,6 cm² h^-1 en diciembre. Espacialmente está "Santiago Puente" (Estación 146) con la mayor erosividad media anual de acuerdo con la intensidad máxima de lluvia en siete minutos que fue 1,659 cm² h^-1, localizado en la parte nordeste de la cuenca. El valor más bajo fue 790 cm² h^-1 en Cuyaguateje (Estación 344) localizada al sur de la región llana (Figura 10). La distribución espacial del índice LAI a lo largo de la cuenca es mostrada en la Figura 11B. Con respecto al índice modificado fournier (23) MFI, de nuevo los valores más altos fueron encontrados en junio (MFI=0,240 mm) y los más bajos en diciembre (MFI=0,005 mm) (Figura 12A).  MFI bien correlacionado con R (2) r= 0,97 y con R (1) r=0,98.

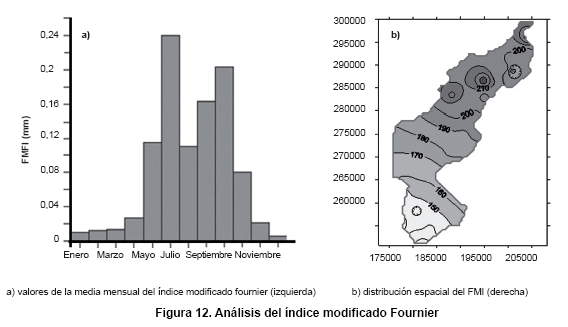
Espacialmente los valores medios anuales de MFI mostraron su máximo valor (230 mm) en Quemado de Pineda (Estación 141) y su mínimo (99 mm) en Cuyaguateje (Estaciónn 394). Esto corresponde a la parte norte y sur de la cuenca respectivamente. La distribución de la media anual de MFI en la cuenca es mostrada en la Figura 12B.

CONCLUSIONES

• Es la primera vez que en esta cuenca y en la parte oeste de Cuba se llevó a cabo un estudio profundo de la erosividad de la lluvia, un paso muy importante en cualquier investigación de la erosión. El trabajo de investigación llevado a cabo es necesario para las obras de erosión sucesivas en la zona.
• Se localizaron las zonas de mayor agresividad de las lluvias, para posteriormente realizar medidas de protección. Alrededor de 96 % de la cuenca Cuyaguateje se ve afectada por muy fuerte erosividad relacionados con la cantidad y la intensidad de las precipitaciones en la cuenca. Los valores medios anuales obtenidos R varía entre 8200 y 18000 MJ mm ha^-1 h^-1 año^-1 por la ecuación de la energía cinética y entre 900 MJ mm ha^-1 h^-1 año^-1 y 22000 MJ mm ha^-1 h^-1 año^-1. Valores muy altos en relación con otros países cuyas condiciones climáticas son muy diferentes a Cuba, como Bélgica y Portugal, con 860 MJ mm ha^-1 h^-1 año^-1 y 3,7418 MJ mm ha^-1 h^-1 año^-1, respectivamente.
• Las ecuaciones de regresión obtenidas anteriormente para la estación V Aniversario fueron validadas por la estación Portales II (estación localizada en la parte sur de la cuenca), para calcular erosividad de 26 estaciones de cuencas, haciendo uso de la cantidad diaria de las precipitaciones, lo que demuestra la veracidad y la aplicabilidad de la metodología propuesta.
• En relación con la distribución, según el año, con una media mensual de erosividad alcanza los valores más altos en junio con R = 2423,1 MJ mm ha^-1 h^-1 y diciembre, el más bajo con R = 171,1 MJ  mmha^-1 h^-1, R (1) = 2,748 MJ mm ha^-1h^-1 y R (1)=279 MJ mm ha^-1 h^-1, respectivamente. Se determinó que existe una alta correspondencia entre la media del factor R mensual y los índices Al_m y MFI con una correlación más de 0,90.
• La distribución espacial de todos los índices de erosividad estudiados varía de los valores más altos en el noreste a valores más bajos en el suroeste de la cuenca, pero la altitud en metros no es un factor determinante en el comportamiento de la precipitación con la correlación entre ambos 0,41.

AGRADECIMIENTOS

El trabajo de investigación se realizó en el marco del proyecto UGent-ZEIN 2005PR306 financiado por la Cooperación Interuniversitario Flamenco-Universidad del Consejo de Desarrollo (VLIR), Bélgica, a la que estamos muy agradecidos.

Notas al pie

^AAlonso, G. Magisterial Conference of the President of Cuban Agency of Environment. (entr. Almoza H. Y.), [Personal Communication], 2011, VII Congress of Cuban Soil Science, La Habana, Cuba.

^BCuban Academic of Science. Hydraulic of Cuyaguateje Watershed. La Habana, Cuba, 2010, pp. 12-20.

^CINRH. Catálogo de Cuencas Hidrográficas Río Cuyaguateje. Inst. National Institute of Hydraulic Resources, Cuba, 2014, p. 6.

BIBLIOGRAFÍA

1. Kinnell, P. I. A. ‘‘Rainfall Intensity-Kinetic Energy Relationships for Soil Loss Prediction’’. Soil Science Society of America Journal, vol. 45, no. 1, 2/01 de 1981, pp. 153-155, ISSN 0361-5995, DOI 10.2136/sssaj1981.03615995004500010033x.

2. Brown, L. C. y Foster, G. R. ‘‘Storm erosivity using idealized intensity distributions’’. Transactions of the American Society of Agricultural Engineers, vol. 30, no. 2, 1987, pp. 379–386, ISSN 0001-2351, 2151-0059.

3. Bandyopadhyay, S.; Ghosh, K. y Kumar, D. S. ‘‘A proposed method of bank erosion vulnerability zonation and its application on the River Haora, Tripura, India’’. Geomorphology, vol. 224, 1 de noviembre de 2014, pp. 111-121, ISSN 0169-555X, DOI 10.1016/j.geomorph.2014.07.018.

4. Schiettecatte, W.; D´hondt, L.; Cornelis, W. M.; Acosta, M. L.; Leal, Z.; Lauwers, N.; Almoza, Y.; Alonso, G. R.; Díaz, J.; Ruíz, M. y Gabriels, D. ‘‘Influence of landuse on soil erosion risk in the Cuyaguateje watershed (Cuba)’’. CATENA, vol. 74, no. 1, 15 de junio de 2008, pp. 1-12, ISSN 0341-8162, DOI 10.1016/j.catena.2007.12.003.

5. Renard, K. G. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE). edit. U.S. Department of Agriculture, Agricultural Research Service, Washington, DC, 1997, 412 p., ISBN 978-0-16-048938-9.

6. Litschert, S. E.; Theobald, D. M. y Brown, T. C. ‘‘Effects of climate change and wildfire on soil loss in the Southern Rockies Ecoregion’’. CATENA, vol. 118, julio de 2014, pp. 206-219, ISSN 0341-8162, DOI 10.1016/j.catena.2014.01.007.

7. Wischmeier, W. H. y Smith, D. D. Predicting rainfall erosion losses - a guide to conservation planning. (ser. Agriculture Handbooks (USA), no. ser. 537), edit. USDA, Washington, DC, 1978, 62 p., CABDirect2, Record Number 19786726437.

8. Rivera, T. F.; Pérez, N. S.; Ibáñez, C. L. A. y Hernández, S. F. R. ‘‘Aplicabilidad del modelo SWAT para la estimación de la erosión hídrica en las cuencas de México’’. Agrociencia, vol. 46, no. 2, marzo de 2012, pp. 101-105, ISSN 1405-3195.

9. Stroosnijder, L. ‘‘Measurement of erosion: Is it possible?’’. Catena, vol. 64, 2005, pp. 162–173, ISSN 0341-8162.

10. Lal, R. Soil Erosion Research Methods. edit. CRC Press, 1 de mayo de 1994, 356 p., ISBN 978-1-884015-09-0.

11. Salles, C.; Poesen, J. y Sempere-Torres, D. ‘‘Kinetic energy of rain and its functional relationship with intensity’’. Journal of Hydrology, vol. 257, no. 1–4, 1 de febrero de 2002, pp. 256-270, ISSN 0022-1694, DOI 10.1016/S0022-1694(01)00555-8.

12. van Dijk, A. I. J. M.; Bruijnzeel, L. A. y Rosewell, C. J. ‘‘Rainfall intensity–kinetic energy relationships: a critical literature appraisal’’. Journal of Hydrology, vol. 261, no. 1–4, 15 de abril de 2002, pp. 1-23, ISSN 0022-1694, DOI 10.1016/S0022-1694(02)00020-3.

13. Rosewell, C. J. ‘‘Rainfall Kinetic Energy in Eastern Australia’’. Journal of Climate and Applied Meteorology, vol. 25, no. 11, 1 de noviembre de 1986, pp. 1695-1701, ISSN 0733-3021, DOI 10.1175/1520-0450(1986)025<1695:RKEIEA>2.0.CO;2.

14. Smith, J. A. y De Veaux, R. D. ‘‘The temporal and spatial variability of rainfall power’’. Environmetrics, vol. 3, no. 1, 1 de enero de 1992, pp. 29-53, ISSN 1099-095X, DOI 10.1002/env.3170030103.

15. Arnoldus, H. M. J. ‘‘Methodology used to determine the maximum potential average annual soil loss due to sheet and rill erosion in Morocco’’. FAO Soils Bulletins (FAO), no. 34, 1977, pp. 39–51.

16. Lal, R. ‘‘Soil erosion on Alfisols in Western Nigeria: III. Effects of rainfall characteristics’’. Geoderma, vol. 16, no. 5, diciembre de 1976, pp. 389-401, ISSN 0016-7061, DOI 10.1016/0016-7061(76)90003-3.

17. Ramos, M. C. ‘‘Rainfall distribution patterns and their change over time in a Mediterranean area’’. Theoretical and Applied Climatology, vol. 69, no. 3-4, septiembre de 2001, pp. 163-170, ISSN 0177-798X, 1434-4483, DOI 10.1007/s007040170022.

18. Grauso, S.; Diodato, N. y Verrubbi, V. ‘‘Calibrating a rainfall erosivity assessment model at regional scale in Mediterranean area’’. Environmental Earth Sciences, vol. 60, no. 8, 22 de septiembre de 2009, pp. 1597-1606, ISSN 1866-6280, 1866-6299, DOI 10.1007/s12665-009-0294-z.

19. Diodato, N. y Bellocchi, G. ‘‘Environmental implications of erosive rainfall across Mediterranean’’. En: eds. Halley G. T. y Fridian Y. T., Environmental impact assessments, edit. NOVA Publishers, New York, USA, 2010, pp. 75–101, ISBN 0-08-02-215900.

20. Salako, F. K. ‘‘Development of isoerodent maps for Nigeria from daily rainfall amount’’. Geoderma, vol. 156, no. 3–4, 15 de mayo de 2010, pp. 372-378, ISSN 0016-7061, DOI 10.1016/j.geoderma.2010.03.006.

21. Abbaspour, K. C.; Faramarzi, M.; Ghasemi, S. S. y Yang, H. ‘‘Assessing the impact of climate change on water resources in Iran’’. Water Resources Research, vol. 45, no. 10, 1 de octubre de 2009, ISSN 1944-7973, DOI 10.1029/2008WR007615, [Consultado: 27 de enero de 2016], Disponible en: <http://onlinelibrary.wiley.com/doi/10.1029/2008WR007615/abstract>.

22. Asadi, H.; Rouhipour, H.; Rafahi, H. G. y Ghadiri, H. ‘‘Testing a Mechanistic Soil Erosion Model for Three Selected Soil Types from Iran’’. Journal of Agricultural Science and Technology, vol. 10, no. 0, 27 de enero de 2010, pp. 79-91, ISSN 1680-7073.

23. Mati, B. M.; Morgan, R. P.; Gichuki, F. N.; Quinton, J. N.; Brewer, T. R. y Liniger, H. P. ‘‘Assessment of erosion hazard with the USLE and GIS: A case study of the Upper Ewaso Ng’iro North basin of Kenya’’. International Journal of Applied Earth Observation and Geoinformation, vol. 2, no. 2, 2000, pp. 78-86, ISSN 0303-2434, DOI 10.1016/S0303-2434(00)85002-3.

24. Angima, S. D.; Stott, D. E.; O’Neill, M. K.; Ong, C. K. y Weesies, G. A. ‘‘Soil erosion prediction using RUSLE for central Kenyan highland conditions’’. Agriculture, Ecosystems & Environment, vol. 97, no. 1–3, julio de 2003, pp. 295-308, ISSN 0167-8809, DOI 10.1016/S0167-8809(03)00011-2.

25. Martinez, D. y Gori, E. G. ‘‘Raindrop size distributions in convective clouds over Cuba’’. Atmospheric Research, vol. 52, no. 3, septiembre de 1999, pp. 221-239, ISSN 0169-8095, DOI 10.1016/S0169-8095(99)00020-4.

26. FAOClim. World-Wide Agroclimatic Data Base. versión 2.02, [Windows 95/98/NT 4/2000/XP], 2003.

27. Mueller, E. A. Raindrop distributions at Miami, Florida. edit. Illinois State Water Survey, Meteorological Laboratory, University of Illinois, Urbana, 1962, 281 p.

28. Yu, B.; Hashim, G. M. y Eusof, Z. ‘‘Estimating the R-factor with limited rainfall data: A case study from Peninsular Malaysia’’. Journal of Soil and Water Conservation, vol. 56, no. 2, 4 de enero de 2001, pp. 101-105, ISSN 0022-4561, 1941-3300.

29. Yu, B. ‘‘Rainfall erosivity and its estimation for Australia’s tropics’’. Australian Journal of Soil Research, vol. 36, no. 1, 1 de enero de 1998, pp. 143-166, ISSN 0004-9573.

30. da Silva, A. M. ‘‘Rainfall erosivity map for Brazil’’. CATENA, vol. 57, no. 3, 22 de agosto de 2004, pp. 251-259, ISSN 0341-8162, DOI 10.1016/j.catena.2003.11.006.

31. Carvalho, N. de O. Hidrossedimentologia prática [en línea]. 2.^a ed., edit. Interciencia, 1994, 372 p., [Consultado: 1 de febrero de 2016], Disponible en: <https://books.google.com.br/books/about/Hidrossedimentologia_pr%C3%A1tica.html?hl=pt-BR&id=TP4cHQAACAAJ>.

32. Winchell, M. F.; Jackson, S. H.; Wadley, A. M. y Srinivasan, R. ‘‘Extension and validation of a geographic information system-based method for calculating the Revised Universal Soil Loss Equation length-slope factor for erosion risk assessments in large watersheds’’. Journal of Soil and Water Conservation, vol. 63, no. 3, 5 de enero de 2008, pp. 105-111, ISSN 0022-4561, 1941-3300, DOI 10.2489/jswc.63.3.105.

Recibido: 2 de diciembre de 2014
Aceptado: 29 de octubre de 2015

Yeleine Almoza Hernández, Universidad Agraria de la Habana, Grupo de Investigaciones Agrofísicas, Autopista Nacional km 23 y 1/2, San José de las Lajas, Mayabeque, Cuba. Email: madehp@infomed.sld.cu