Transformación de variables binomiales para su análisis según un diseño de bloques al azar
Transformation of binomial variables for analysis according to a randomized block design
Dr.C. Edison Ramiro Vásquez,I Dr.C. Alberto Caballero Núñez,II Magaly Herrera VillafrancaIII
IUniversidad Nacional de Loja, Ecuador.
IIUniversidad Técnica de Manabí, Ecuador.
IIIInstituto Nacional de Ciencia Animal, Cuba.
Resumen
La investigación tuvo como objetivo valorar la transformación de variables con distribución Binomial en diseño de bloques al azar. Para el análisis se consideró 5, 10 y 30 observaciones por unidad experimental (n) y probabilidad de éxito del evento (p) de 0,10; 0,20; … 0,90. Mediante el método de Monte Carlo, se simularon 100 experimentos con tres, cinco y nueve tratamientos (t); cuatro y ocho réplicas (r); con 5, 10 y 30 observaciones por unidad experimental (n) y probabilidad de éxito del evento (p) de 0,10; 0,20; … 0,90. Se evidenció que la transformación angular arcoseno y de la familia de transformaciones de potencia de Box-Cox: logaritmo natural, raíz cuadrada e inversa no fueron capaces de solucionar las desviaciones, respecto a los supuestos del ANAVA. Es preciso mencionar, que en los últimos años se realizan pocos aportes relacionados con este tipo de investigación.
Palabras clave: supuestos ANAVA, Monte Carlo, simulación, variable dicotómica.
ABSTRACT
The research aimed to evaluate the transformation of variables with Binomial distribution applied to randomized block design. For the analysis was considered 5, 10 and 30 observations per experimental unit (n) and probability of success of the event (p) of 0,10; 0,20; ...; 0,90. Through the Monte Carlo method, 100 experiments with 3, 5 and 9 treatments (t) were simulated; 4 and 8 replicates (r); with 5, 10 and 30 observations per experimental unit (n) and probability of success of the event (p) of 0,10; 0,20; ...; 0;90. It was evident that the arcsine and family transformations Box- Cox power transformation angle: natural logarithm, square root and inverse were not able to solve the deviations with respect to the assumptions of ANAVA. It should be mentioned that in recent years little input regarding such research are made.
Key words: ANAVA assumptions, Monte Carlo, simulation, dichotomous variable.
INTRODUCCIÓN
El trabajo del estadístico, de manera conjunta con el investigador, consiste en conseguir un modelo, que refleje en lo posible, la situación planteada y a partir de aquí, aplicar los procedimientos de análisis que más se adecue (1). Sin duda, uno de los modelos más difundidos lo constituye el Análisis de Varianza, el cual utilizado de manera eficiente, se convierte en una poderosa herramienta de análisis. No obstante, esta técnica exige del cumplimiento de ciertos requerimientos de los términos de error aleatorio del modelo lineal como errores independientes, normalmente distribuidos y con varianzas homogéneas para todas las observaciones, condiciones que muchas veces no se cumplen (2–5).
En la práctica investigativa, con frecuencia, se presentan situaciones de variables que pueden, de alguna manera, no satisfacer los requerimientos que el ANAVA exige (6, 7); tal es el caso, de variables de conteos, que por su naturaleza discreta pueden alejarse de la normalidad. En tal sentido se señala (8–11), que dada la “robustez” de la prueba F en este procedimiento de análisis, su incumplimiento no tiene graves consecuencias en el análisis. De igual modo (6), señalan que resulta prácticamente irrelevante en lo referente a la probabilidad de cometer un error tipo I; pues, no se aparta del valor α determinado por el experimentador. Sin embargo, la “robustez” de la prueba puede perderse cuando este incumplimiento es severo, ya que se incrementa la probabilidad de exceder el valor nominal de la prueba (12, 13).
Dada su naturaleza y frecuente existencia en muchas ramas de la ciencia, son de importancia aquellas variables de conteos que provienen de variables dicotómicas o distribución binomial, en las que se establece una estrecha relación de dependencia entre varianza y media de tratamientos; aspecto que puede estar presente en otro tipo de variables (14). Por tanto, es de suponer que de presentarse diferencias entre las medias en cada variante que se están ensayando, sean posibles diferencias entre sus respectivas varianzas y con ello el no cumplimiento de este supuesto.
Son muchos los aspectos que puede recibir el impacto desfavorable cuando se incumplen estos supuestos, entre otros: el porcentaje en que se rechaza la hipótesis nula; la diferencia mínima que se puede detectar entre medias de tratamientos; la potencia observada del ANAVA; número de rechazo de igualdad de medias de tratamientos. De aquí que identificar, tener en cuenta y conocer su grado de afectación, revista gran importancia.
Para incrementar la eficiencia del tratamiento estadístico en investigaciones con variables con distribución Binomial en el modelo de Análisis de Varianza, se puede recurrir al empleo de alternativas, como transformación de datos y métodos estadísticos no paramétricos.
En este contexto, en el presente artículo se pretende valorar el impacto de las transformaciones de variables con distribución binomial aplicado al diseño de bloques al azar.
MATERIALES Y MÉTODOS
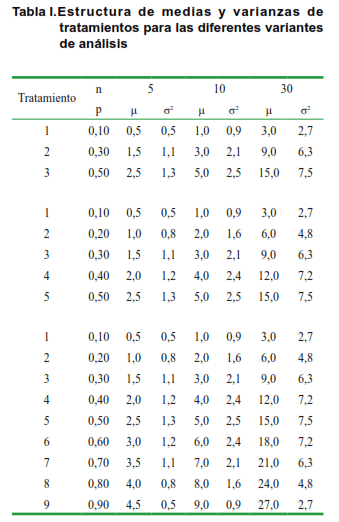
Para cumplir con el objetivo propuesto se utilizó el proceso de Simulación de Monte Carlo (15–18) para generar poblaciones de variables aleatorias con distribución Binomial con varianzas homogéneas y heterogéneas, según prueba de Levene (19) a p<0,05 para 5, 10 y 30 observaciones por unidad experimental (n) y probabilidad de éxito del evento de 0,10, 0,20, …, 0,90 (p). Se conformaron experimentos en Diseño Bloques al Azar con tres, cinco y nueve tratamientos (t); cuatro y ocho réplicas (r). La combinación de medias de los tratamientos se definió de modo tal, que las diferencias entre estas medias fueran detectables por la prueba Mínima Diferencia Significativa (DMS) a un nivel de significación del 0,05 (Tabla I); para cada combinación t-r-n, se generaron 100 experimentos.
A los datos con distribución Binomial con varianzas heterogéneas y homogéneas, se les aplicó la transformación angular arcoseno, por ser la transformación sugerida para este tipo de datos (20) y de la familia de transformaciones de potencia de Box-Cox: logaritmo natural, raíz cuadrada e inversa, que resultaron ser las sugeridas con mayor frecuencia en los experimentos analizados.
Se utilizó la prueba de Comparación de Proporciones con el fin de contrastar la diferencia entre el porcentaje de experimentos con distribución Binomial de referencia y con las transformaciones angular y de potencia Box-Cox para experimentos con varianza entre tratamientos homogénea y heterogénea.
RESULTADOS Y DISCUSIÓN
Se discute el comportamiento de algunos indicadores estadísticos que se relacionan con los supuestos teóricos del ANAVA: porcentaje de experimentos que muestran asimetría en la distribución, correlación entre media y varianza de tratamientos e independencia de sus errores experimentales.
Experimentos asimétricos
En la Tabla II se muestra los resultados de las variables con distribución Binomial para tres, cinco y nueve tratamientos; se observa que el 80 % de los experimentos tuvieron un comportamiento asimétrico para tres y cinco tratamientos, independientemente de la homocedasticidad, lo cual se debe a que las poblaciones que conforman ambos grupos de experimentos fueron generadas con parámetros p menores a 0,50. Sin embargo, al utilizar nueve tratamientos se evidencia que los experimentos asimétricos no superaron el 15 %, dado que estos experimentos fueron generados con p próximo a 0,50; esto está asociado a la influencia de este parámetro en la característica de la distribución de probabilidad de la variable Binomial (21).
En general, para experimentos con valores del parámetro p menores a 0,50 (tres y cinco tratamientos), en los cuales su asimetría, desde el punto de vista teórico, es más acentuada, aunque presenten o no homogeneidad en sus varianzas, la transformación angular arcoseno redujo el porcentaje de experimentos asimétricos con respecto a la variable Binomial sin transformar, lo cual significa un acercamiento a la normalidad del dato transformado, resultado que está acorde con lo reportado por otras investigaciones (22), al destacar lo acertado de esta transformación para datos con distribución binomial. En este contexto, se encontró un comportamiento aceptable de la transformación raíz cuadrada.
Para nueve tratamientos, donde la asimetría es menos severa, la transformación arcoseno, provoca desviaciones notables de la normalidad, cuando se compara con el dato sin transformar, como también sucede con todas las demás transformaciones de potencias de Box-Cox; esto constituye una alerta del peligro a que se exponen el investigador y el experto estadístico, si deciden una transformación, sin llevar a cabo un análisis crítico de la situación concreta que enfrenta (23).
Relación entre media y varianza
En la Tabla III, se aprecia que ni la transformación angular, así como ninguna de las transformaciones de potencia, lograron romper las relación entre media y varianza en experimentos de datos con distribución binominal, aunque posean o no varianzas homogéneas, entre sus tratamientos. Más aún, para los experimentos con nueve tratamientos, en los cuales la asimetría es menos acuciante, las transformaciones de potencia acentuaron la relación entre estos dos parámetros de la distribución.
Estos resultados discrepan con los obtenidos por otros autores (24), pues, a más de eliminar la dependencia existente entre media y varianza, lograron estabilizar la varianza de poblaciones de insectos, mediante el empleo de algunas transformaciones de potencias. Sin embargo, al utilizar un conjunto de transformaciones de potencia, no se logró romper la relación de dependencia entre estos dos parámetros, en datos provenientes de una población de insectos que se ajustaba a una distribución Binomial Negativa (25).
Independencia de errores
En la Tabla IV se observa que para las variables binomiales, el porcentaje de experimentos que presentan ausencia de correlación de primer orden en sus errores, se mantuvo entre el 60 y el 80 %, independientemente del cumplimiento o no del supuesto de homocedasticidad, aspecto que puede estar asociado con la propia definición y naturaleza de estas variables, en el que su varianza es función directa de su media.
Ninguna de las transformaciones de potencia, ni la propia transformación angular fueron capaces de dar solución a la presencia de correlación entre los errores. Esto no debe ser interpretado como un desacierto solo de la transformación, dado que existen otras causas con efecto no despreciable en la desviación de este supuesto a tener en cuenta, como el emanado del propio diseño de la investigación, lo cual se puede resolver con una acertada recomendación sobre el rediseño de la investigación.
CONCLUSIÓN
De modo general, un análisis integral de los indicadores: asimetría, relación media-varianza e independencia de errores, evidenció que las transformaciones aplicadas no fueron capaces de solucionar las desviaciones, respecto a estos supuestos del ANAVA, lo que coincide con lo reportado por otros investigadores (24), que encontraron que de la totalidad de los trabajos analizados a los que se practicó una transformación de potencia, sólo en el 10 % de ellos, se logró satisfacer el cumplimiento de los supuestos, y en más del 28 %, se les aplicó la transformación indebidamente. En este sentido, no siempre las transformaciones son capaces de solucionar a los incumplimientos de los supuestos teóricos del ANAVA, relacionados con los indicadores estudiados.
BIBLIOGRAFÍA
1. Ramiro, V. E. y Caballero, N. A. “Cuando falla el supuesto de homocedasticidad en variables con distribución binomial”. Cultivos Tropicales, vol. 32, no. 3, 2011, pp. 191-199, ISSN 0258-5936.
2. Di Rienzo, J. A.; Casanoves, F.; González, L. A.; Tablada, E. M.; Díaz, M. del P.; Robledo, C. W. y Balzarini, M. G. Estadística para las ciencias agropecuarias [en línea]. 7.a ed., Ed. Brujas, 2008, Córdoba, 356 p., ISBN 978-1-4135-7950-5, [Consultado: 18 de noviembre de 2016], Disponible en: <http://public.eblib.com/choice/publicfullrecord.aspx?p=3185731>.
3. Herrera, V. M.; Guerra, B. C. W.; Sarduy, G. L.; García, H. Y. y Martínez, C. E. “Diferentes métodos estadísticos para el análisis de variables discretas. Una aplicación en las ciencias agrícolas y técnicas”. Revista Ciencias Técnicas Agropecuarias, vol. 21, no. 1, 2012, pp. 58-62, ISSN 2071-0054.
4. Wiedenhofer, H. Pruebas no paramétricas para las ciencias agropecuarias. Muestras pequeñas. 2.a ed., Ed. Instituto Nacional de Investigaciones Agrícolas, 2013, Maracay, Venezuela, 261 p., ISBN 978-980-318-284-7.
5. Guerra, B. C. W.; Herrera, V. M.; Vázquez, A. Y. y Quintero, B. A. B. “Contribución de la Estadística al análisis de variables categóricas: Aplicación del Análisis de Regresión Categórica en las Ciencias Agropecuarias”. Revista Ciencias Técnicas Agropecuarias, vol. 23, no. 1, 2014, pp. 68-73, ISSN 2071-0054.
6. Sokal, R. R. y Rohlf, F. J. Biometry: the principles and practice of statistics in biological research. 4.a ed., Ed. W.H. Freeman, 2012, New York, 937 p., ISBN 978-0-7167-8604-7.
7. Pedrosa, I.; Juarros, B. J.; Robles, F. A.; Basteiro, J. y García, C. E. “Pruebas de bondad de ajuste en distribuciones simétricas, ¿qué estadístico utilizar?”. Universitas Psychologica, vol. 14, no. 1, 2015, pp. 245-254, ISSN 1657-9267, DOI 10.11144/Javeriana.upsy13-5.pbad.
8. Wetherill, G. B. Intermediate statistical methods. Ed. Chapman and Hall, 1981, London, 390 p., ISBN 978-0-412-16440-8.
9. Mendeş, M. y Yiğit, S. “Comparison of ANOVA- F and ANOM tests with regard to type I error rate and test power”. Journal of Statistical Computation and Simulation, vol. 83, no. 11, 2013, pp. 2093-2104, ISSN 0094-9655, 1563-5163, DOI 10.1080/00949655.2012.679942.
10. Ostertagová, E. y Ostertag, O. “Methodology and Application of Oneway ANOVA”. American Journal of Mechanical Engineering, vol. 1, no. 7, 2013, pp. 256-261, ISSN 2328-4102, 2328-4110, DOI 10.12691/ajme-1-7-21.
11. Schmider, E.; Ziegler, M.; Danay, E.; Beyer, L. y Bühner, M. “Is It Really Robust?: Reinvestigating the Robustness of ANOVA Against Violations of the Normal Distribution Assumption”. Methodology, vol. 6, no. 4, 2015, pp. 147-151, ISSN 1614-1881, 1614-2241, DOI 10.1027/1614-2241/a000016.
12. Arnau, J.; Bendayan, R.; Blanca, M. J. y Bono, R. “Efecto de la violación de la normalidad y esfericidad en el modelo lineal mixto en diseños split-plot”. Psicothema, vol. 24, no. 3, 2012, pp. 449-454, ISSN 0214-9915.
13. Hecke, T. V. “Power study of anova versus Kruskal-Wallis test”. Journal of Statistics and Management Systems, vol. 15, no. 2-3, 2012, pp. 241-247, ISSN 0972-0510, 2169-0014, DOI 10.1080/09720510.2012.10701623.
14. McDonald, J. H. Handbook of biological statistics [en línea]. 3.a ed., Ed. Sparky House Publishing, 2014, Baltimore, Maryland, 299 p., [Consultado: 18 de noviembre de 2016], Disponible en: <http://www.biostathandbook.com/HandbookBioStatThird.pdf>.
15. Robert, C. P. y Casella, G. Monte Carlo Statistical Methods [en línea]. (ser. Springer Texts in Statistics), 2.a ed., Ed. Springer, 2004, New York, 645 p., ISBN 978-1-4419-1939-7, [Consultado: 18 de noviembre de 2016], Disponible en: <http://link.springer.com/10.1007/978-1-4757-4145-2>.
16.Rubinstein, R. Y. y Kroese, D. P. Simulation and the Monte Carlo method. Ed. John Wiley & Sons, 2008, Hoboken, N.J., 345 p., ISBN 978-0-470-17794-5.
17. Ortiz, J. E. y Moreno, E. C. “¿Se necesita la prueba t de Student para dos muestras independientes asumiendo varianzas iguales?”. Comunicaciones en Estadística, vol. 4, no. 2, 2011, pp. 139-157, ISSN 2027-3355, DOI 10.15332/s2027-3355.2011.0002.05.
18. Peña, D. Fundamentos de estadística [en línea]. Ed. Alianza Editorial, 2014, Madrid, España, 683 p., ISBN 978-84-206-8877-0, [Consultado: 18 de noviembre de 2016], Disponible en: <http://alltitles.ebrary.com/Doc?id=11028686>.
19. Levene, H. “Robust tests for the equality of variance” [en línea]. En: Olkin I., Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling, Ed. Stanford University Press, 1960, pp. 278-292, ISBN 978-0-8047-0596-7, [Consultado: 3 de junio de 2016], Disponible en: <https://books.google.com.cu/books?id=ZUSsAAAAIAAJ>.
20. Mead, R.; Curnow, R. N. y Hasted, A. M. Statistical methods in agriculture and experimental biology. 3.a ed., Ed. Chapman & Hall/CRC, 2002, Boca Raton, FL, 472 p., ISBN 978-1-58488-187-2.
21. Sachs, L. Applied Statistics: A Handbook of Techniques [en línea]. 2.a ed., Ed. Springer Science & Business Media, 2012, 737 p., ISBN 978-1-4612-5246-7, Google-Books-ID: A0bhBwAAQBAJ, [Consultado: 18 de noviembre de 2016], Disponible en: <https://books.google.com.my/books?id=A0bhBwAAQBAJ&hl=es&source=gbs_book_other_versions>.
22. Hogg, R. V.; McKean, J. y Craig, A. T. Introduction to Mathematical Statistics [en línea]. 7.a ed., Ed. Pearson, 2012, Boston, 640 p., ISBN 978-0-321-79543-4, [Consultado: 18 de noviembre de 2016], Disponible en: <https://www.amazon.com/Introduction-Mathematical-Statistics-Robert-Hogg/dp/0321795431>.
23. de Calzadilla, J.; Guerra, W. y Torres, V. “El uso y abuso de transformaciones matemáticas. Aplicaciones en modelos de análisis de varianza”. Cuban Journal of Agricultural Science, vol. 36, no. 2, 2002, pp. 103-106, ISSN 0034-7485.
24. Verghese, A.; Tandon, P. L. y Rao, G. S. P. “Ecological studies relevant to the management of Thrips palmi Karny on mango in India”. Tropical Pest Management, vol. 34, no. 1, 1988, pp. 55-58, ISSN 0143-6147, DOI 10.1080/09670878809371207.
25. Cabrera, A.; Guerra, W. y Surís, M. “Selección de modelos de regresión para describir el patrón espacial de Thrips palmi Karny (Thysanoptera: Thripidae) en el cultivo de papa”. Cultivos Tropicales, vol. 23, no. 4, 2002, pp. 77–83, ISSN 1819-4087.
Recibido: 29/07/2015
Aceptado: 27/05/2016
Dr.C. Edison Ramiro Vásquez, Universidad Nacional de Loja, Ecuador. Email: edison.vasquez@outlook.com